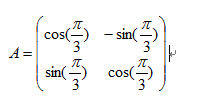1. 介绍

摘自维基：
科赫曲线是一种分形，是de Rham曲线的特例。
给定线段AB，科赫曲线可以由以下步骤生成：
1.将线段分成三等份（AC,CD,DB）
2.以CD为底，向外（内外随意）画一个等边三角形DMC
3.将线段CD移去
4.分别对AC,CM,MD,DB重复1~3。
科赫雪花是以等边三角形三边生成的科赫曲线组成的。每条科赫曲线的长度是无限大，它是连续而无处可微的曲线。

2. 数学原理与Matlab实现

摘自分形系列之matlab绘制koch曲线
1 . 算法分析：

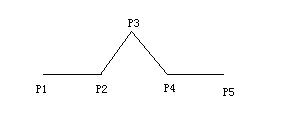
描述

描述

在直线段的中间依次插入三个点P2，P3，P4。P2,P4三等分点。P3是P2,P4中点，旋转60°由正交矩阵实现。

旋转矩阵
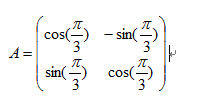
根据初始数据（P1和P5点的坐标），产生图中5个结点的坐标。结点的坐标数组形成一个矩阵，矩阵的第一行为P1的坐标，第二行为P2的坐标……，第五行为P5的坐标。矩阵的第一列元素分别为5个结点的x坐标，第二列元素分别为5个结点的y坐标。
进一步考虑Koch曲线形成过程中结点数目的变化规律。设第k次迭代产生的结点数为n(k)，第k+1次迭代产生的结点数为n(k+1)，则n(k)和n(k+1)中间的递推关系为n(k+1)=4n(k)-3。

2 . 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
function Koch(num)
p = [0 0;10 0];%p初始线段两端点
n=2;  %n结点数
A=[cos(pi/3) -sin(pi/3);sin(pi/3) cos(pi/3)]; %旋转矩阵
for k=1:num   %k为分形次数
 d=diff(p)/3;%diff计算相邻两个点的坐标之差 d得三等分点
 m=4*n-3;%迭代公式
 q=p(1:n-1,:); %以原点为起点,前n-1个点的坐标为终点形成向量
 p(5:4:m,:)=p(2:n,:); %迭代后处于4k+1位置上的点的坐标为迭代前的相应坐标
 p(2:4:m,:)=q+d;     %用向量方法计算迭代后处于4k+2位置上的点的坐标    
 p(3:4:m,:)=q+d+d*A';  %用向量方法计算迭代后处于4k+3位置上的点的坐标   
 p(4:4:m,:)=q+2*d;   %用向量方法计算迭代后处于4k位置上的点的坐标
 n=m; %迭代后新的结点数目
end
plot(p(:,1),p(:,2));
axis([0 10 0 10]);
matlab演示

matlab演示

3. Javascript实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <title>KochCurve</title>
</head>
<body onload="Draw()">
<form >
    <label>请选择分形次数</label>
    <input type="range" name="points" min="1" max="9" onchange="change()" id="range">
    <input type="text" id="show">
    <input type="button" value="Draw" onclick="Draw()"/>
</form>
<br/>
<canvas id="myCanvas" width="600" height="600"
        style="border: 1px solid #c3c3c3;background-color: antiquewhite">
    Your browser does not support the canvas element.
</canvas>

<script type="text/javascript">
    var c = document.getElementById("myCanvas");
    var cxt  = c.getContext("2d");

    /*科赫曲线函数*/
    function Koch(p1,p2,n){

        if(n==0){
            drawLine(p1.x,p1.y,p2.x,p2.y);
            return;
        }

        var p3 = {}, p4={}, p5 = {};
        var d53x,d53y;

        p3.x = (2*p1.x + p2.x) / 3;
        p3.y = (2*p1.y + p2.y) / 3;
        p5.x = (p1.x + 2*p2.x) / 3;
        p5.y = (p1.y + 2*p2.y) / 3;

        d53x = (p2.x - p1.x)/3;
        d53y = (p2.y - p1.y)/3;

        p4.x = p3.x+ d53x* Math.cos(Math.PI/3) +d53y*Math.sin(Math.PI/3);
        p4.y = p3.y- d53x* Math.sin(Math.PI/3) +d53y*Math.cos(Math.PI/3);

        Koch(p1,p3,n-1);
        Koch(p3,p4,n-1);
        Koch(p4,p5,n-1);
        Koch(p5,p2,n-1);
    }

    function Draw(){
        clearCanvas();
        var n=parseInt(document.getElementById("range").value);  //传入分形次数

        //返回元素的高度和宽度，以像素为单位。
        var osa={x:0,y:c.offsetHeight / 2};
        var osb={x:c.offsetWidth,y:c.offsetHeight / 2};

        Koch(osa, osb, n);
    }

    /*canvas连线*/
    function drawLine(x0,y0,x1,y1){
        cxt.beginPath();
        cxt.strokeStyle ="00ff00";
        //cxt.lineWidth = 2;
        cxt.moveTo(x0,y0);
        cxt.lineTo(x1,y1);
        cxt.stroke();
    }

    /*清空画布*/
    function clearCanvas() {
        cxt.clearRect(0,0,c.width,c.height);
    }

    /*滑块数字显示*/
    function change(){
        var num = document.getElementById("range");
        var location = document.getElementById("show");
        location.value = num.value;
    }
</script>

</body>
</html>